
推 ainamk: 「無理數的數量跟有理數的數量中間有沒有別的無限」 05/16 19:12
推 hutao: 對於那些主張正解應該是無法比較而不是一樣多的有何看法 05/16 19:13
請他們找個數學老師問。
→ ainamk: 這個問題的結論好像也是讓數學界很頭大 05/16 19:13
推 Lisanity: 你很厲害www 05/16 19:13
※ 編輯: zax8419 (116.89.129.129 臺灣), 05/16/2023 19:14:02
推 Lass1n: 你好認真 05/16 19:14
推 fman: 趕快推不然被人發現我看不懂 05/16 19:15
推 gox1117: 跟文組解釋那麼多幹嘛== 05/16 19:15
推 CATALYST0001: 每次都覺得數學才是真正的玄學== 05/16 19:15
→ CATALYST0001: 我不能只會微積分跟傅立葉變換就好了嗎:( 05/16 19:16
→ chordate: 質數無限多個這個高中就有證了 05/16 19:16
→ chordate: 至於要證質數和自然數一樣多可沒有這麼簡單 05/16 19:17
→ chordate: 要找到bijection 05/16 19:17
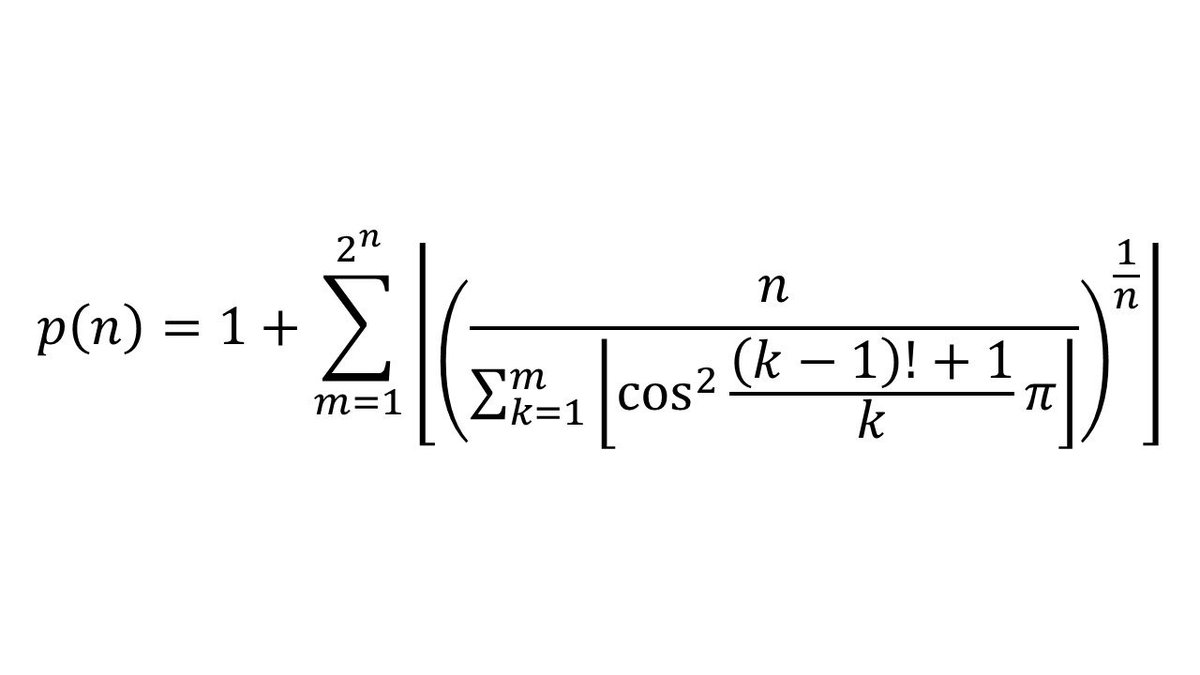
→ ainamk: 代自然數n進去會生出第n個質數的謎公式 05/16 19:20
推 HAmakers: 想起以前考資工所離散數學的數論 真的不知道在供三小 05/16 19:20
推 smart0eddie: 嗯嗯 跟我想的一樣 05/16 19:22
推 sunshinecan: 推個 05/16 19:22
推 Mormory: 那什麼神祕公式啦 XDDDD 05/16 19:25
→ chordate: 另外一個比容易的方法,就是找兩個1-1函數 05/16 19:26
推 Rust: 證這個不需要用複雜的公式啊 只要有演算法算出第N個質數就 05/16 19:27
→ Rust: 好了 有人問為何是bijection就說是一個一個數的 05/16 19:27
→ Rust: 另外一樓說的是連續統假設 在ZFC內無法證明也無法證否 05/16 19:28
推 ainamk: 樓上你不要再加新名詞了 到時候有人好奇ZFC是什麼XD 05/16 19:31
推 poornow: x=0 05/16 19:32
推 alfa871212: 講的不錯 易懂 05/16 19:33
→ chordate: 因為質數是自然數子集,一邊的1-1很容易 05/16 19:39
→ chordate: 另外一邊就用Well-ordering principle可以做出來 05/16 19:39
推 lightKevin: 好 我問 ZFC是什麼 05/16 19:42
推 opeminbod001: 講中文啦 乾 05/16 19:42
→ chordate: ZFC就是現在數學最常用的公理系統 05/16 19:46
→ CATALYST0001: 那有KFC嗎? 05/16 19:46
推 ainamk: ZFC的概念就是把早期數學中發現的重要邏輯矛盾補起來 05/16 19:47
推 Rust: 有人會問公理系統是什麼 05/16 19:47
推 a1487546: 推,寫的蠻好懂的 05/16 19:48
推 wohtp: 都在算第一個質數、第二個質數了,這不是bijection什麼才是 05/16 19:48
推 ryu1735: 推推文 05/16 19:48
→ chordate: 不是,證明不能直接說第一個第二個,因為說第一個第二 05/16 19:49
→ chordate: 個隱含的意思就是你找到一個函數對應自然數和質數 05/16 19:50
→ chordate: 你要真的把拿個函數做出來才是證明 05/16 19:50
我是覺得啦 除非是本科系的 不然越講越細節只會讓大家越來越排斥數學
唉 數學其實很有趣的
推 ainamk: (指指我po的圖) 05/16 19:50
→ Rust: 如果是找一對反函數 函數用演算法的形式寫出呢 05/16 19:53
推 Orangekun: 我以為不能直接用第1、2、3個來證明,而是要證明一一 05/16 19:55
→ Orangekun: 對應的關係才能知道他們是一樣多?例如自然數跟偶數一 05/16 19:55
→ Orangekun: 樣多可以符合n與2n,有幾個自然數就有幾個偶數這樣 05/16 19:55
科普向的就別要求那麼多了
你要我全部完整寫出來就也沒人要看了(實話是我也懶得寫)
推 zseineo: 雖然是不懂數學但看一些科普書真的覺得數學就是魔法 05/16 19:55
※ 編輯: zax8419 (116.89.129.129 臺灣), 05/16/2023 19:58:06
推 ainamk: 就算喜歡數學也不見得會想要自己跳下去完整解題老實講XD 05/16 20:02
推 kankandara: 有一個旅館 每個房間都有一個不重複的自然數編號 今天 05/16 20:05
→ kankandara: 來了一群客人 每位客人都有一個質數編號 每位客人都 05/16 20:05
→ kankandara: 要住進字面上等同自己編號的房間 所有客人check in 完 05/16 20:05
→ kankandara: 成後 空房間是無限的嗎?有住人的房間是否遠少於沒住 05/16 20:05
→ kankandara: 人的房間? 05/16 20:05
→ kankandara: (客人的質數編號也相互不重複) 05/16 20:06
推 oToToT: 謝謝你希爾伯特 05/16 20:08
推 abadjoke: 淺顯易懂 05/16 20:11
推 NicoNeco: 所有質數的乘積+1 不一定是質數吧? 05/16 20:15
這邊要先注意到前提 是"質數為有限多個"
而這個乘積+1 除以 任何一個質數均是餘一
其他所有的合數也可以視為質數的乘積(可以質因數分解)
從定義上 這一個數的正因數僅有"1"與"自己"時 就是個質數
那這個N+1就會是個質數
※ 編輯: zax8419 (116.89.129.129 臺灣), 05/16/2023 20:19:30
推 GaoLinHua: 有無限的房間卻常常客滿的飯店 05/16 20:19
推 AirO0264400: 0..0 05/16 20:21
推 Hosimati: 假設有n個質數 1.其實還有第n+1個質數可以整除N+1 2.N+ 05/16 20:22
→ Hosimati: 1是質數 05/16 20:22
推 gsmfrsf: 謝謝你數學人 看到推文那個公式有個cos我更不懂了 05/16 20:26
推 leo125160909: 感謝科普 05/16 20:31
→ GodVoice: 我把標題改寫一下 應該就能讓人懂了吧 05/16 20:31
→ GodVoice: 1000個自然數跟 1000個質數 誰比較多??? 05/16 20:31
五公斤的棉花 跟五公斤的鐵塊 誰比較重
※ 編輯: zax8419 (116.89.129.129 臺灣), 05/16/2023 20:32:33
推 inte629l: 推個 以前修過數學系的數學導論,後來就聳了... 05/16 20:35
→ inte629l: 是說ZFC好像是集合論會帶到的東西? 05/16 20:35
推 ainamk: 其實反證法這東西即使是理工科的人也有不小比例搞不懂… 05/16 20:35
推 gs8613789: 黃子嘉有教過 05/16 20:37
推 lancelot123: 1樓說的那個東西是戴德金分割,已經有證明了 05/16 20:52
推 ainamk: 樓上你再看清楚一點我寫的東西是什麼XD 05/16 20:53
推 rey123123: 你好棒 05/16 20:54
→ chordate: Dedekind cut是講實數完備性 05/16 20:55
→ chordate: 跟不連續統假設是兩件事 05/16 20:56
推 liweitsai: 講的很有道理 對吧發仔 05/16 20:59
推 rjaws: 以中學數學來說,你寫的很棒,好懂又沒省略太多 05/16 21:03
推 Darnatos: 嗯嗯 就是這樣 05/16 21:09
推 nisioisin: 寫得蠻好理解的耶 05/16 21:52
推 papple23g: 推 05/17 00:02
推 NicoNeco: OKOK 懂了 永遠都有更大的質數所以是無限多個質數這樣 05/17 00:22
→ NicoNeco: 文章看太快 05/17 00:22
推 cn5566: 那個公式也太鬼了 05/17 00:38
推 Matsumatsu: 好懷念 是我高中的東西 05/17 00:41
推 YeaPa: 這我也會 第一題 trivial 第二題我會但是推文寫不下 05/17 01:05
推 SKY25desert: 專業 05/17 01:12
推 fth862: 不是我不在乎 是我看不太懂 我知道你講中文 但是合在一起 05/17 07:58
→ fth862: 像外星人講話 05/17 07:58
推 qaz86368: 數學系 覺得這篇講的滿淺白的 以科普的角度來看其實不 05/17 08:23
→ qaz86368: 錯 05/17 08:23
推 hw1: 我剛剛還以為我在八卦 特地看作者是不是張阿月 05/17 16:35
推 cwmd86124: 雖然跟主題沒什麼關係,不過QED的D後面要加點喔,它跟 05/18 09:56
→ cwmd86124: RIP的P一樣很容易被忘記 05/18 09:56
















